Luento 23.4. Koneoppiminen II

Luennon aluksi muisteltiin edellisen viikon asioita lyhyesti, mm. Matlab-demoa, jolla voidaan piirtää hiirellä projektiosuora kaksiulotteisen datan koordinaatistoon. Kun kaksi pistettä suoralta on merkitty, Matlab-skripti projisoi datan tälle suoralle ja piirtää tuloksena saatavien yksiulotteisten näytteiden jakauman sekä luokitteluprosentin. Hyvillä projektiosuorilla data oli täydellisesti luokiteltavissa, mutta huonoilla joukot menivät päällekkäin projisoinnin jälkeen. Fisherin lineaarinen erottelija laskee tämän suoran automaattisesti niin että erottelu on optimaalinen.

Tukivektorikone ja logistinen regressio ovat myös lineaarisia luokittimia, mutta niiden opetusalgoritmi on eri kuin LDA:n. Tukivektorikoneen erityispiirre on sen käyttö yhdessä kernelitempun kanssa ja logistisen regression ominaisuutena on sen todennäköisyystulkinta: LR antaa myös luokan todennäköisyyden, ei pelkästään ennustettua luokkaa.

Tämän jälkeen paneuduttiin hermoverkkoihin sekä niiden opetukseen, ja mainittiin  lyhyesti opetusalgoritmin perustuvan derivaattaan ja ketjusääntöön. Näiden avulla voidaan päätellä suunta, jossa luokitteluvirhe pienenee jyrkimmin, ja kyseiset kaavat löytyvät esim. täältä. Perus-backpropagationin lisäksi on olemassa kehittyneempiä ja nopeampia opetusalgoritmeja, ja esim. Matlabissa niitä on lähes parikymmentä. Olennaisin ero algoritmien välillä on niiden nopeudessa ja muistin tarpeessa.
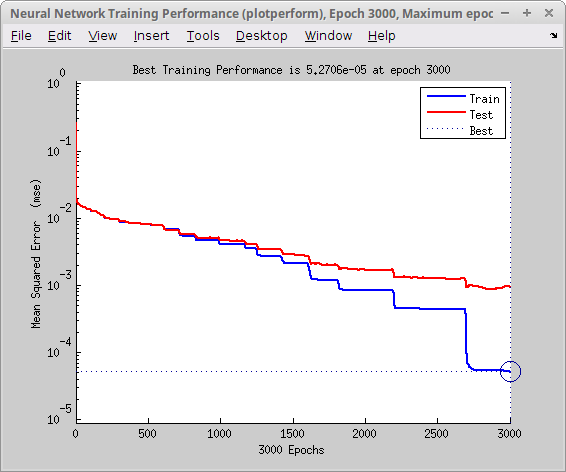
Luentotauolla Matlabilla opetettiin hermoverkko, joka osasi tunnistaa eurooppalaisista rekisterikilvistä kerättyjä merkkejä.Opetus kesti noin 15 minuuttia, ja virheen kehittyminen on esitetty oikealla olevassa kuvassa. Opetuksen aikana mitattiin luokittelijan virhettä opetusaineistossa (10 000 merkkiä) sekä erillisessä testiaineistossa (1 000 merkkiä). Kuvasta nähdään että virhe oli selvästi pienempi opetusaineistolla kuin testijoukossa. Ilmiöstä käytetään nimeä ylioppiminen, ja se tarkoittaa että järjestelmä alkaa oppia opetusaineiston epäolennaisia ja satunnaisia ominaisuuksia, jotka eivät ole yleisesti voimassa. Ensisijainen ratkaisu tähän on lisätä opetusmateriaalin määrää (joko todellisella uudella datalla tai augmentoimalla käytettävissä olevaa dataa; esim. venyttelemällä kuvia, lisäämällä kohinaa jne.).
 
Viime perjantaina verkkoa testattiin esimerkkikuvilla, joista näytettiin hiirellä merkin sijainti. Testissä havaittiin luokittelun toimivan täysin oikein kun merkki oli hyvin laatikon sisällä. Jos merkin lisäksi 10x10-laatikon sisällä oli muutakin, luokittelu meni väärin.
Tavallisen hermoverkon herkkyys merkin oikealle kohdistukselle on yleinen ongelma. Tämä on saatu valtaosin ratkaistua uudemmissa ns. konvoluutioverkoissa, jotka esiteltiin alun perin jo 1980-luvulla, mutta ovat saavuttaneet valtavan suosion vasta laskentatehon lisäännyttyä 2010-luvulla. Syvät (yli 3 tasoa; jopa 1000 tasoa) konvoluutioverkot ovat aiheuttaneet läpimurron kuvan- ja puheentunnistuksessa.

Lopuksi vilkaistiin tuoreita esimerkkejä syvillä hermoverkoilla saavutetuista tuloksista:

• Image captioning, joka generoi kuvasta tekstimuotoisen kuvauksen.
• @DeepDrumpf, joka generoi Tweettejä Donald Trumpilta oppimallaan tyylillä.
• Microsoftin rohkea mutta valitettavasti hyökkäyksen kohteeksi joutunut Tay-botti. [The Vergen artikkeli; ei lapsille]
• TTY:n iänarviointidemo. 
• Kissan muuttaminen koiraksi.
• DeepFakes.

Luento 20.4. Koneoppiminen I

Tänään aloitimme kappaleen 11, joka käsittelee hahmontunnistusta. Hahmontunnistusjärjestelmän ideana on esittää järjestelmälle näytteitä ja opettaa se tuottamaan oikea ulostulo kun sille esitetään opetusjoukkoon kuulumaton uusi näyte. Yksi oppivien järjestelmien osajoukko ovat luokittelijat, jossa ulostulo kertoo luokan johon esitetty näyte kuuluu.

Suosittuja luokittelualgoritmeja ovat ainakin seuraavat (kasvavan monimutkaisuuden järjestyksessä):

• k-nearest neighbor eli KNN
• Lineaarinen luokittelija eli LDA eli Fisherin diskriminantti
• Logistinen regressio
• Tukivektorikone (support vector machine); SVM
• Hermoverkot; NN

Näistä kaksi ensimmäistä käsiteltiin luennolla. KNN on ideana yksinkertaisin: kaikki opetusdata pidetään muistissa ja uuden näytteen tullessa etsitään k samanlaisinta näytettä, ja valitaan näistä yleisin luokka. Tyypillisesti k on vajaan kymmenen luokkaa, mutta voi olla suurempikin; esim. 30. Mitä suurempi k on, sitä sileämpi luokkarajasta tulee. Vaikka KNN:n luokittelutulos onkin melko hyvä, on sen ongelmana suuri muistin tarve sekä laskennallinen kompleksisuus. Koko opetusjoukko täytyy nimittäin säilyttää muistissa, josta etsitään k lähintä naapuria jokaisen luokittelun yhteydessä. Sekä tilantarve että etsinnän vaatima aika voivat olla ongelmallisia jos opetusjoukossa on esim. 100000 alkiota.

Luentomonisteen seuraava menetelmä on Fisherin diskriminantti eli LDA. Tätä voidaan havainnollistaa alla olevalla Matlab-demolla, jossa näkyy erilaisia projektiosuoria kaksiulotteisen datan koordinaatistossa. Suoran suunta vaihtelee ja tuloksena piirretään alle näin saatavien yksiulotteisten näytteiden jakauma sekä luokitteluprosentti. Hyvillä projektiosuorilla data oli täydellisesti luokiteltavissa, mutta huonoilla joukot menivät päällekkäin projisoinnin jälkeen. Fisherin lineaarinen erottelija laskee tämän suoran automaattisesti niin että erottelu on optimaalinen. Suora ratkaistaan maksimoimalla ns. Fisherin suhde (näkyy myös kuvassa alla), joka kertoo kuinka hyvin tulosjoukot erottuvat toisistaan (isompi parempi). Oikessa tilanteessa paras suunta ratkaistaan suljetussa muodossa olevan kaavan avulla eikä kokeilemalla (mikä olisikin mahdotonta 1000-ulotteiselle datalle).



Taustoitettaessa koneoppimista vilkaistiin demoa jossa hermoverkko tunnistaa hiirellä osoitetun merkin rekisterikilvestä. Ks. myös tämä demo. Lisäksi mainittiin tamperelainen Visy Oy, joka tekee automaattista rekisterikilven tunnistusta mm. Hämpin parkissa.

Luento 16.4. Näytteenottotaajuuden muuntelun sovelluksia

Tänään käsiteltiin näytteenottotaajuuden muuntelu yksityiskohtaisemmin. Aluksi ratkaistiin tentin 05/14 tehtävä 4, ja selvitettiin kuinka desimointi 48000 Hz -> 6000 Hz kannattaa tehdä. Vaihtoehdothan ovat 

• 48000 Hz -> 6000 Hz (suoraan)
• 48000 Hz -> 12000 Hz -> 6000 Hz (kahdessa vaiheessa)
• 48000 Hz -> 24000 Hz -> 12000 Hz -> 6000 Hz (kolmessa vaiheessa)

Suunnittelimme jokaiseen tapaukseen tarvittavat suotimet, ja laskimme paljonko ne tarvitsevat yhteensä kertolaskuja per sekunti. Kävi ilmi että kolmessa vaiheessa tehtävä desimointi on nopein (yli 6x nopeampi kuin suora toteutus).

Toisella tunnilla tutkittiin muunnosta rationaalikertoimilla (esim. 5/4). Yhdistämällä interpolointi ja desimointi päästään yksinkertaisempaan rakenteeseen huomaamalla kokonaisuudessa olevan kaksi suodatinta peräkkäin, jotka molemmat poistavat tietyn kaistan ylätaajuuksilta. Näin ollen vain toinen niistä on tarpeellinen. Piirtämällä kuva näiden suodinten amplitudivasteista voidaan päätellä kumpi on tarpeeton (aina se, jota vastaava muunnoskerroin on isompi).

Toisen tunnin lopuksi tutustuttiin interpoloinnin sovellukseen D/A-muunnoksessa. Menetelmää käytettiin jo ensimmäisissä CD-soittimissa 1980-luvun alussa ja sen ideana on tehostaa nollannen asteen pitopiirin toimintaa nostamalla näytteenottotaajuus korkeammaksi ennen pitopiiriä. Tämä näkyy aikatasossa porraskuvion hienontumisena ja tätä kautta pitopiirin virheen pienenemisenä jä siirtymisenä korkeammille taajuuksille. Taajuustasossa yli 22,05 hertsin taajuuksille tulee vastaavia heijastuksia kuin interpoloinnin yhteydessäkin. Erona on, että nyt heijastumat vaimenevat sitä enemmän mitä korkeammalle mennään. Digitaalinen interpolointi helpottaa näiden heijastusten poistamista: ilman digitaalista interpolointia tarvittavan analogisen suotimen siirtymäkaistan leveys olisi 2,05 kHz (20kHz...22.05kHz), kun esim. nelinkertaisella interpoloinnilla se saadaan yli 130 kHz:n levyiseksi (väli 20kHz...154,35 kHz).

Luento 13.4. Äärellisen sananpituuden vaikutukset; näytteenottotaajuuden muuntelu

Tänään tarkasteltiin äärellisen sanapituuden vaikutuksia. Tarkastelimme ensin mallia, jolla johdettin arvio AD-muunnoksen kvantisointivirheen varianssille, joka on suoraan verrannollinen syntyvän kvantisointivirheen tehoon. Tätä kautta määritellään SNR, eli signaali-kohinasuhde, eli häiriöetäisyys. Tämä suure kertoo jotain äänenlaadusta, ja saatavia tuloksia tullaan tarvitsemaan kappaleessa 9, kun päätellään montako bittiä signaalista uskalletaan poistaa kompressiossa ilman äänenlaadun havaittavaa heikkenemistä.

Jos ehtojen oletetaan olevan voimassa, voidaan osoittaa kohinan odotusarvon olevan nolla ja varianssin yhtä kuin 2^(-2b) / 12.

Yllä olevaa kaavaa voidaan edelleen jalostaa signaali-kohinasuhteen käsitteeksi (SNR), joka kertoo signaalin tehon suhteessa kohinan tehoon. Kun kaavaa pyöriteltiin, havaittiin jokaisen ylimääräisen bitin (per näyte) nostavan SNR:ää kuudella desibelillä.

Lopuksi johdettiin kaava varianssille suodatuksen jälkeen ja sekä tutkittiin suotimen kertoimien pyöristämisen vaikutusta. Tämähän täytyy tehdä aina kun suodin toteutetaan huonomman tarkkuuden alustalla kuin Matlab (esim. tällä 17-bittisellä DSP:llä).

Toislla tunnilla tutustuttiin desimointi- ja interpolointi-operaatioihin, jotka toimivat kokonaislukukertoimilla. Näitä yhdistelemällä saadaan kaikki rationaalikertoimet. Molemmat operaatiot tarvitsevat alipäästösuodattimen, joka on yleensä FIR, ja suunnitellaan normaaleilla menetelmillä. Suotimen siirtymäkaistasta todettiin, että se laitetaan aina rajataajuuden alapuolelle. Näin signaaliin tulee vähemmän virhettä kuin jos laskostumista pääsisi tapahtumaan.

Desimoinnissa tapahtuva näytteenottotaajuuden pieneminen toteutetaan yksinkertaisesti jättämällä näytteitä pois tasaisin väliajoin. Esimerkiksi kertoimella kolme jätetään vain joka kolmas näyte jäljelle. Tämä kuitenkin aiheuttaa laskostumista, koska signaalin sisältämät taajuudet pysyvät samoina mutta näytteenottotaajuus pienenee. Tämä saadaan luonnollisesti estettyä suodattamalla signaali ennen alinäytteistämistä sopivalla alipäästösuotimella.
Interpolointi puolestaan koostuu nollien lisäämisestä sekä tämän operaation tuottamien roskien poistamisesta. Nollien lisääminenhän tuottaa kopioita ja peilikuvia alkuperäisestä spektristä, jotka voidaan myös poistaa kätevästi alipäästösuodatuksella. Oikealla olevassa kuvassa on luennolla ollut esimerkki näytteenottotaajuuden kolminkertaistamisesta, jossa kahden näytteen väliin sijoitetaan aina 2 nollaa (yläkuva). Alakuvassa on tuloksen spektrogrammi, jossa näkyy selkeästi kolme versiota alkuperäisestä (kaista 0-4000 Hz) taajuuskaistasta (kopio-peilikuva-kopio).

Luento 9.4: IIR-suodinten suunnittelu

Kappaleessa 6 esitetään menetelmiä IIR-suodinten suunnitteluun, ja ne käydään melko yleisellä Matlab-komentojen osaamisen tasolla. Kappaleen ydin on koottu monisteen taulukkoon, jossa suodintyyppejä vertaillaan amplitudivasteen ominaisuuksien ja kertoimien määrän suhteen. Kertoimia tarvitaan eri menetelmillä 29+28, 13+12 ja 8+7 kappaletta. Suurin määrä tulee Butterworth-suotimella ja pienin elliptisellä suotimella. Kahden Chebyshev-suotimen kerroinmäärä on näiden kahden ääripään välissä. Vertailun vuoksi FIR-suotimen kertoimien määrä vastaavilla vaatimuksilla olisi N = [5.5/0.035] = 159 käytettäessä Blackman-ikkunaa.

Muita luennolla esiin tulleita seikkoja olivat mm.

• Matlabin kerroinvektorit a ja b eivät ole suoraan käytettävissä ulostulon y(n) laskennassa, vaan takaisinkytkentäkertoimien (siis esim. termin y(n-1) kertoimen) merkki täytyy vaihtaa vastakkaiseksi.

• Elliptisellä suotimella on aina vähemmän kertoimia kuin muilla. Lisäksi tasavärähtely-ominaisuus on yleensä hyvä asia.

IIR-suotimen etuna on siis pienempi kertoimien tarve. Haittapuolina mahdollinen epästabiilisuus sekä numeeriset ongelmat toteutuksessa. Tästä esimerkkinä on esim. kurssin SGN-16006 signaaliprosessorityö, jossa täytyy toteuttaa IIR-suodin. Käytännössä yli toisen asteen IIR-suodinta ei voi toteuttaa numeeristen ongelmien vuoksi. Sen sijaan suodin täytyy jakaa peräkkäisiin toisen asteen lohkoihin esim. Matlabin TF2SOS-funktiolla. 

Toisella tunnilla käsiteltiin äärellisen sananpituuden vaikutuksia. Meidän tarkastelussamme nämä ilmenevät A/D-muunnoksen yhteydessä sekä suodatettaessa äärellisellä laskentatarkkuudella. Pääpaino on ensimmäisessä tyypissä. Luennolla käsiteltiin näytteistyksessä käytettävät kvantisointitasot: esimerkiksi (1+7) bitin esityksessä käytettävissä ovat seuraavat 256 tasoa: -128/128, -127/128, ..., 0, ..., 126/128, 127/128. 
 
Pyöristettäessä lähimpään lukuun syntyvä kvantisointivirhe on aina välillä -1/256...1/256. Yleisesti pyöristys (1+b) bittiin aiheuttaa enintään virheen 2^(-b) / 2 suuntaan tai toiseen. Vasemmalla olevassa kuvassa on esimerkkitapaus jossa "seiska" kvantisoidaan 1+9 bittiin. 

Luento 6.4.: Suodinsuunnittelu käytännössä

Tänään käsiteltiin kappale 5 loppuun. Alussa oli alla olevan kuvan mukainen demo, jossa suotimen kertoimien määrää kasvatettiin ja havaittiin ettei amplitudivastetta saa tällä keinolla tiettyjen rajojen alle.

Tämän jälkeen käytiin kappale 5 loppuun, ja todettiin että suodinsuunnittelu sisältää seuraavat vaiheet. 

1. Valitse ikkuna vaimennusvaatimusten perusteella.
2. Päättele tarvittava kertoimien määrä N siirtymäkaistan leveyden (delta_f) perusteella.
3. Laske ideaalinen impulssivaste (vaatii siirtymäkaistan keskipisteen f_c laskennan).
4. Kerro ideaalinen impulssivaste valitun ikkunafunktion lausekkeella.

Taululla ratkaistiin elokuun 2016 tentin tehtävä 4, jossa suodinsuunnittelu tehdään alusta loppuun paperilla. Yleisiä tentissä esiintyviä virheitä ovat:

1. Muuttujat f_c ja delta_f sekoittuvat keskenään
2. Käytetään normalisoimattomia taajuuksia (esim. 12000 eikä 12000/32000)
3. Rajataajuudet on laskettu väärin tai sekoitettu keskenään.
4. Ikkuna on valittu väärin tai N on laskettu väärin.
5. Lopputuloksessa on avoimia muuttujia (f_c, delta_f tai N). 

Tunnin lopuksi tutustuttiin IIR-suotimiin. Kappaleessa 6 esitetään menetelmiä IIR-suodinten suunnitteluun, ja ne käydään melko yleisellä Matlab-komentojen osaamisen tasolla. Lopuksi suunniteltiin Butterworth-tyyppinen IIR-suodin Matlabilla.

Luento 26.3: Suodinsuunnittelu

Tänään tutustuttiin suodinsuunnitteluun ikkunamenetelmällä. Suunnittelukriteerit ovat kahtalaiset: suotimen taajuusvasteen määräämiseksi pitää tietää millainen vaihevaste halutaan ja millainen amplitudivaste halutaan.

Vaihevasteen osalta vaaditaan että kaikkien taajuuksien tulee viivästyä yhtä paljon. Tämä toteutuu jos vaihevaste on lineaarinen. Yksinkertaisimmissa tapauksissa vaihevasteen lauseke voi olla siis esimerkiksi muotoa -2w, joka taatusti on lineaarinen. Matlabissa tällainen kuvaaja saadaan esim. komennoilla:

>> [H,W] = freqz([1, 2, 1]);
>> plot(angle(H));
>> grid on

Tälle suotimelle laskettiin vaihevaste myös analyyttisesti taululla.

Freqz-funktiosta saa siis ulos taajuusvastefunktion arvoja vektorissa H. Vektorissa on lueteltu taajuusvasteen kompleksiset lukuarvon 512:ssa pisteessä taajuusakselilla. 


Amplitudivasteen osalta tavoitteena on saada vaste päästökaistalla ykköseksi ja estokaistalla nollaksi. Käytännössä tämä ei ole mahdollista, vaan suotimelle täytyy antaa hieman toleranssia ja sallia tietty määrä värähtelyä molemmilla kaistoilla. Lisäksi kaistojen väliin täytyy sallia "don't care" -alue, jossa amplitudivaste saa olla mitä vain.

Prujussa ratkaistaan mikä impulssivaste toteuttaisi ideaalisen amplitudivasteen (arvot vain nollaa tai ykköstä). Osoittautuu että impulssivasteen muoto on tuttu sinc-funktio, mutta sen pituus on ääretön. Tämän vuoksi suotimesta ei saataisi ainuttakaan vastearvoa koskaan, vaan laskentaa tarvittaisiin äärettömän paljon.

Tästä ongelmasta päästään katkaisemalla impulssivaste, mutta tämä luonnollisesti vaikuttaa amplitudivasteeseen. Oikealla olevan kuvan mukaisen demottiin, että suoralla katkaisulla ei estokaistan värähtelyä saada millään alle n. 21 desibelin, ja päästökaistallakin suurin heitto on luokkaa 0.7 dB. Ratkaisu tähän on käyttää ikkunointia, eli kertoa katkaistu impulssivaste jollain ikkunafunktiolla. Näin voidaan päästä parempiin vaimennusominaisuuksiin.

Ideaalisen suotimen impulssivasteen pituus on ääretön, eikä sitä voi käytännössä toteuttaa. Näin ollen impulssivaste on katkaistava, mistä seuraa vääristymä amplitudivasteeseen. Oikealla olevasta kuvasta nähdään, että tätä ei voi kompensoida esim. kertoimia lisäämällä, vaan on käytettävä ikkunaa, joka pehmentää katkaisun vaikutusta. Ikkunoita on lueteltu esim. sivun 84 taulukossa, ja mitä paremmat vaimennusominaisuudet niillä on, sitä leveämpi siirtymakaistasta tulee. Onneksi tätä voidaan kuitenkin kompensoida kertoimia lisäämällä.

Luento 23.3. Z-muunnoksen laskenta ja suotimen analyysi

Tänään käsiteltiin suotimen analysointi (kappale 4) melkein loppuun.

Menetelmässähän ratkaistaan ensin impulssivaste, sitten siirtofunktio ja lopuksi taajuusvaste. Taajuusvaste on kompleksifunktio, joten sitä ei voida sellaisenaan piirtää 2-ulotteiseen koordinaatistoon. Näin ollen piirretään kaksi kuvaajaa: funktion itseisarvon kuvaaja sekä sen vaihekulman kuvaaja. Näistä edellinen kertoo kuinka paljon eri taajuuksien amplitudit muuttuvat suodatuksessa ja jälkimmäinen paljonko ne viivästyvät suodatuksessa. Amplitudivaste on näistä mielenkiintoisempi, koska sen avulla taajuuksia saadaan esim. poistettua yksinkertaisesti huolehtimalla että amplitudivaste ko. taajuudella on nolla.Vaihevaste puolestaan kertoo paljonko eri taajuudet viivästyvät suodatettaessa.

Amplitudivastetta tarkasteltaessa on kätevämpi käyttää desibeliasteikkoa, joka on logaritminen. Logaritmi tekee kertolaskusta yhteenlaskua, ja korostaa lähellä nollaa olevia eroja, jotka molemmat ovat meille käteviä ominaisuuksia.

Kappaleen 4 kaksi viimeistä lukua käytiin läpi ratkaisemalla kevään 2009 lokakuun tentin tehtävä 3. Tässä tehtävässä on annettu suotimen yhtälö, josta täytyy ratkaista siirtofunktio, piirtää napa-nollakuvio sekä päätellä stabiilisuus. Maanantaina ratkaistaan vielä löydetyn siirtofunktion arvo taajuudella 2500 Hz (tentin bonustehtävä).

Luennolla nähtiin demo, jossa tutkittiin taajuusvasteen visualisointia alemman animaation mukaisesti. Vasemman yläkulman kuvaajassa ovat kaikki termit exp(-iwk), jotka on kerrottu suotimen kertoimilla oikean yläkulman kuvassa (siis h(k)exp(-iwk)). Näiden summa vektoriesityksenä on puolestaan vasemmassa alakulmassa, jonka etäisyys origosta (amplitudivaste) on kuvattu alaoikealla.

Luento 19.3. Z-muunnos

Tänään tarkasteltiin Z-muunnosta ja sen tärkeimpiä ominaisuuksia. Z-muunnoksen avulla voidaan selvittää mm. suotimen stabiilisuus: suodin on stabiili jos kaikki siirtofunktion navat ovat yksikköympyrän sisäpuolella.

Tässä yhteydessä tutkittiin myös napa-nollakuvion ja taajuusvasteen suhdetta. Tästä nähtiin alla olevan kuvan mukainen demo, jossa hiirellä voidaan sijoitella napoja ja nollia yksikköympyrälle. Alimpaan kuvaan piirtyy jokaisen klikkauksen jälkeen suotimen amplitudi- ja taajuusvasteet; niin että jokainen nolla aiheuttaa sakaran alaspäin ja jokainen napa huipun ylöspäin.
Opiskelimme myös Z-muunnoksen laskentaa esimerkkisignaalien tapauksessa. Erityisesti keskityimme prujun esimerkkisuotimen analyysiin: johdimme Z-muunnoksen suotimen yhtälöstä, ja jatkoimme taajuusvasteen, amplitudivasteen ja vaihevasteen laskentaan.

Luento 16.3: FFT-algoritmi

Tänään tarkasteltiin Fourier-muunnoksen ominaisuuksia, sovelluksia sekä nopeaa toteutusta.

Luennon aluksi käytiin läpi v. 2016 elokuun tentin tehtävä 2b, jossa laskettiin käsin neljän mittainen Fourier muunnos (ks. myös videon esimerkki). 

Seuraavaksi tutustuttiin Fourier-muunnoksen käyttöön alkeellisessa puheentunnistimessa. Kirjan Elements of statistical learning kappaleen 5.2.3 inspiroimana toteutin Matlab-skriptin, joka löytää S-kirjaimet mikrofonin taltioimasta puheesta. Menetelmä on nimeltään logistinen regressio, joka monimutkaisista kaavoista huolimatta on varsin yksinkertainen toteuttaa: menetelmä etsii kertoimet kullekin Fourier-muunnoksen taajuudelle, ja laskee tulokset yhteen. Tuloksen perusteella saadaan todennäköisyys kummallekin luokalle: "S" ja "ei-S".

Menetelmää demottiin Matlab-toteutuksella, jossa luokittelija opetettiin erottamaan S-äänne muista äänteistä näyttämällä luokittimelle esimerkkejä kahteen luokkaan kuuluvista Fourier-muunnoksista. Menetelmä toimi kohtalaisen hyvin ottaen huomioon opetusaineiston erot testiaineistoon. Matlab-koodi löytyy alta.
 
Esimerkki kuvaa hyvin tämän päivän signaalinkäsittelyalgoritmia: perusmenetelmiä (Fourier-muunnos, konvoluutio, jne.) käytetään piirregeneraattoreina, jotka tuottavat hieman parempaa raakadataa kuin suora mittaussignaali (esim. taajuustietoa eikä raakaa mittausdataa). Laskettujen piirteiden perusteella sitten nostetaan tiedon abstraktiotasoa edelleen. Esimerkiksi äänteen tunnistuksessa hierarkia on esimerkiksi seuraava:

16000 aikatason näytettä -> 128 taajuustason kerrointa -> 1 bitti, joka kertoo kumpi äänne on kyseessä

Tämän jälkeen siirryttiin tarkastelemaan Fourier-muunnoksen ominaisuuksia. Ominaisuuksista tutustuttiin lähemmin siirtoon ajassa (esim. laske signaalin x(n+20) muunnos, kun tiedetään x(n):n muunnos) sekä konvoluution muunnokseen (DFT muuntaa konvoluution kertolaskuksi, eli x(n)*y(n) -> X(n)Y(n)). Aivan luennon lopussa mainittiin yhteys ns. dekonvoluutioon joka on konvoluutiolle käänteinen operaatio. Menetelmää käytetään muun muassa matkaviestinnän siirtotien häiriöiden korjaukseen sekä Hubble-teleskoopin alkuaikoina, jolloin yhdessä peilissä olleen hiontavirheen vuoksikuvat olivat sumuisia. Kuvantamisprosessia voidaan nimittäin mallintaa (kaksilulotteisella) konvoluutiolla

y(n,m) = h(n,m) * x(n,m),

missä x on todellinen näkymä, y on havaittu sumuinen kuva, ja h on linssin impulssivaste (nk. point spread function; PSF). Yhtälössä y ja h ovat tunnettuja, ja tehtävänä on ratkaista x. Ratkaisu löytyy taajuustasossa, koska

Y(n,m) = H(n,m) X(n,m),

joten (Matlabin syntaksilla ilmaistuna):

x(n,m) = ifft (Y(n,m) ./ H(n,m)).

Dekonvoluutiosta on hyötyä yleisemminkin lineaarisen kanavan aiheuttaman häiriön poistossa. Jos tiedetään signaalin x kulkeneen kanavan h läpi, voidaan vastaanotetusta mittaustuloksesta y päätellä x, jos meillä on joku käsitys kanavasta h. Esimerkkinä tästä on esim.mainittu  langattoman tiedonsiirtokanavan estimointi ja sen aiheuttaman vääristymän kompensointi.

Toinen menetelmän tuottama etu on että Fourier-muunnoksen (käytännössä FFT:n) avulla voidaan laskea konvoluutio kaavasta (Matlabin syntaksilla ilmaistuna):

conv(x,y) = ifft(fft(x) .* fft(y))

Lisäksi käsiteltiin nopeaa Fourier-muunnosta eli FFT:tä, joka on vain nopeampi tapa toteuttaa diskreetti Fourier-muunnos (DFT). FFT perustuu signaalin jakamiseen lyhyempiin pätkiin, jotka muunnetaan jakamalla ne edelleen rekursiivisesti kahtia. Rekursio päättyy, kun muunnoksen pituus on 1, jolloin muunnosta ei tarvitse enää tehdä. 1-ulotteisen vektorin tapauksessa muunnosmatriisi on yksinkertaisesti F = [1], joka tarkoittaa pelkkää ykkösellä kertomista eikä sitä tarvitse tehdä. Lyhyemmistä vektoreista saadaan koostettua pidemmät vektorit kaavoilla (3.3) ja (3.4).

Alla on vielä luennon esimerkkikoodi S-kirjaimen tunnistuksesta. Funktio käyttää Stanfordin yliopistossa kehitettyä glmnet-pakettia. Jos näiden asennus on haastavaa, Matlabissa on nykyään myös valmis glmfit-funktio.
 

function vokaalin_tunnistus()
%
% Esimerkki vokaalin ja S-kirjaimen erottelusta äänisignaalista.
% heikki.huttunen@tut.fi -- 4.2.2015
%

close all

addpath /home/hehu/Documents/Libraries/glmnet_matlab/

% Ladataan opetusaineisto:

[x, Fs] = audioread('seiska.wav');

[X, H, numFrames] = extractFeatures(x, Fs);
title ('Merkitse S-kirjaimet hiirella');

isConsonant = zeros(numFrames, 1);

while true
    
    [x1, y1] = ginput(1);
    [x2, y2] = ginput(1);
    
    if x1 > x2
        xt = x1;
        x1 = x2;
        x2 = xt;
    end
    
    isConsonant(round(x1 * numFrames) : round(x2 * numFrames)) = 1;
    
    response = questdlg('Jatketaanko annotointia?', ...
        'Kysymys', ...
        'Kyllä', 'Ei', 'Kyllä');
    
    if strcmp(response, 'Ei')
        break
    end
    
end

cvob2 = cvglmnet(X, isConsonant, 'binomial', [], 'class');
yHat = glmnetPredict(cvob2.glmnet_fit, X, cvob2.lambda_min, 'response');

coefficients = H * cvob2.glmnet_fit.beta(:, cvob2.lambda == cvob2.lambda_min);

figure()
subplot(211)
plot(yHat);
ylabel('S-kirjaimen TN')
subplot(212)
stem(coefficients)

response = questdlg('Valmiina tunnistamaan?', ...
        'Tunnistus', ...
        'OK', 'OK');

while true
    
    close all

    myRecObj = audiorecorder(Fs, 16, 1);
    recordblocking(myRecObj, 2);
    y = getaudiodata(myRecObj);

    X = extractFeatures(y, Fs);
    yHat = glmnetPredict(cvob2.glmnet_fit, X, cvob2.lambda_min, 'response');

    figure()
    plot(yHat);

    response = questdlg('Jatketaanko tunnistusta?', ...
        'Kysymys', ...
        'Kyllä', 'Ei', 'Kyllä');
    
    if strcmp(response, 'Ei')
        break
    end
    
end

end

function [F, H, numFrames] = extractFeatures(x, Fs)

    [~,f,t,S] = spectrogram(x, 256, 128, 256, Fs, 'yaxis');
    surf(t, f, 10*log10(abs(S)), 'EdgeColor', 'none');
    axis xy; axis tight; colormap(jet); view(0,90);

    S = log10(S)';
    
    H = [];
    n = (1:size(S, 2))';
    
    for k = 0:3
        H = [H, n.^k];
    end
    
    F = S * H;
    numFrames = size(S, 1);
    
end

Luento 12.3.: konvoluutio ja Fourier-muunnos

  
Luennon aluksi käsiteltiin kappale 2 loppuun. Tällöin tutustuttiin konvoluution ominaisuuksiin (laskentasäännöt: a(b+c) = ab+ac, kausaalisuuden ja stabiilisuuden tunnistus impulssivasteesta, jne.). Konvoluution ominaisuuksien käsittelyn yhteydessä tuotiin esille niiden yhteys LTI-järjestelmien yhdistämiseen: peräkkäiset tai rinnakkaiset LTI-järjestelmät voidaan esittää yhtenä järjestelmänä ja toisaalta niiden järjestys ei vaikuta lopputulokseen.

Kappaleen lopussa määriteltiin FIR- ja IIR-suotimet LTI-järjestelmien alalajeina. FIR-suotimet ovat yksinkertaisuutensa vuoksi laajemmin käytettyjä, mutta IIR-suodinten ilmaisuvoima ja laskennallinen tehokkuus tekevät niistä hyödyllisiä useissa tilanteissa.

Testikysymys: onko seuraava suodin FIR vai IIR?

   y(n) = 0.9 y(n-1) - y(n-2) + x(n) + 0.5 x(n-1) +2 x(n-2)

Haastavampaa on selvittää esim. se, onko yo. suodin stabiili. Tähän ratkaisu löytyy prujun sivulta 68, johon pääsemme aikanaan.

Toisella tunnilla päästiin kappaleeseen 3: Fourier-muunnos. Olennaisin asia käsitteli muunnoksen ideaa alla olevan kuvan mukaisesti. Fourier-muunnoksen idea on kysyä paljonko eri taajuuksia annetussa signaalissa on. Taululla oli alla olevan piirroksen kaltainen kuva. Kuvan "yhtälössä" vasemmalla oleva signaalin pätkä jaetaan eri taajuuksiin kysymällä paljonko tarvitaan vakiotaajuutta (0.3 kpl), paljonko kerran värähtävää siniä (0.6 kpl), jne. Sama idea on kaikkien neljän muunnostyypin takana, mutta erona on montako eri taajuutta tarvitaan muodostamaan alkuperäinen signaali. Joissain tapauksissa niitä tarvitaan äärettömän paljon, jolloin kuvan summan sijaan tarvitaan integraali.

Jatkuvat tapaukset perustuvat siis integraalin laskentaan, ja käytännössä tämä täytyy tehdä muunnostaulukoiden avulla.

 

Tarkkaan ottaen yllä olevan kuvan sinisignaalit eivät riitä esittämään kaikkia mahdollisia signaaleita: lisäksi tarvitaan mahdollisuus viivästää tai edistää eri taajuuksia. Tämä onnistuu laajentamalla taajuuksien kokoelma kompleksiksi eksponenttisignaaleiksi: exp(ix) = cos(x) + i sin(x). Kompleksinen eksponenttifunktio on oheisen kuvan mukainen, eli sen reaaliosa ja imaginaariosa värähtelevät samalla taajuudella.

Käsin laskettavien kolmen ensimmäisen muunnostyypin jälkeen tutustuttiin lopuksi diskreettiin Fourier-muunnokseen, joka voidaan esittää matriisimuunnoksena. Muunnosmatriisi muodostetaan lisäämällä rivi kerrallaan ykkösen n:nnen juuren eri potensseja. Lopuksi esitettiin tällaisen matriisin konstruointi yksikköympyrän avulla tapaukselle N = 4.